Left Linear Grammar to Finite Automata

For Complete YouTube Video: Click Here

In this class, We discuss Left Linear Grammar to Finite Automata.

The reader should have prior knowledge of how to convert finite automata to left linear grammar Click Here.

Given below is the Left Linear Grammar.

C – C1 | B1

B – A1 | 1

A – A0 | C0 | B0 | 0

The language accepted by the left linear grammar is a set of strings containing the last two characters 11.

First step: Reverse the given left linear grammar. We get the Right linear grammar.

The below grammar is the reverse of the given left linear grammar.

C – 1C | 1B

B – 1A | 1

A – 0A | 0C | 0B | 0

The above right linear grammar will accept the strings containing the reverse of the given language.

Now we construct finite automata for the right linear grammar.

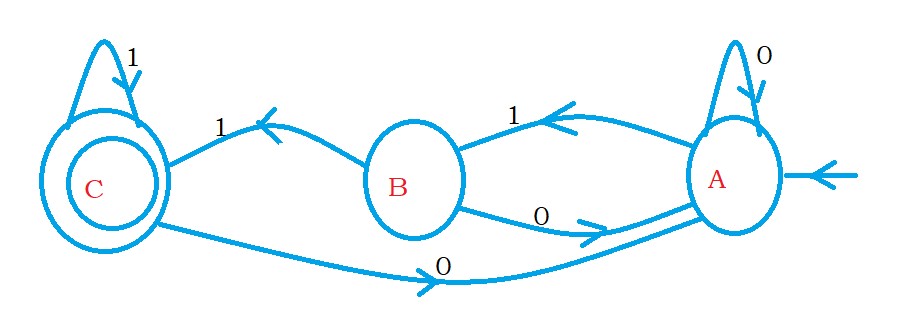
The below diagram shows the finite automata for right linear grammar.

The final state is A.

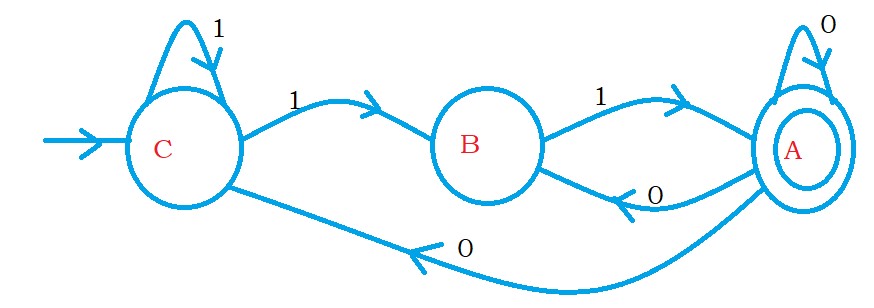
Now we need to reverse the finite automata.

To reverse the finite automata, change initial state to final state and final state to initial state and reverse the arrows.

The below diagram shows the finite automata after reverse.