Minimization of DFA Non Reachable States Example

For Complete YouTube Video: Click Here

In this class, We discuss the Minimization of DFA Non Reachable States Example.

The reader should have prior knowledge of the minimization of the DFA example. Click Here.

In the previous class, We explained the procedure to minimize the DFA.

This class is one more practice example with non-reachable states.

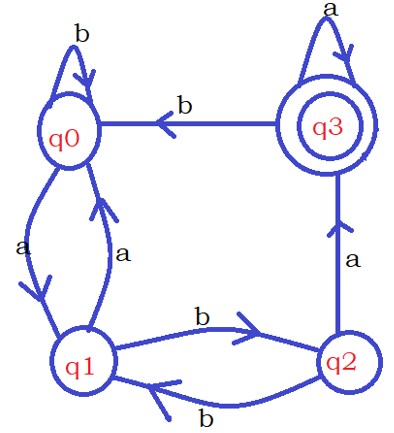
Consider the below DFA example.

The DFA contain state q3 as non-reachable.

So we remove the state q3 and the transition of the state q3.

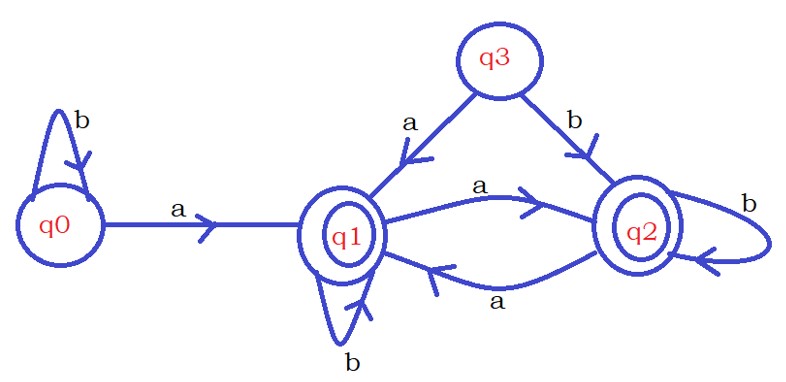
The below diagram shows the DFA after removing the state q3.

The next step, we consider final states as one set and non-final states as another set.

In our example, q0 is the non-final state. q1 and q2 are final states.

The non-final state is named Q1, and the final states are called Q2.

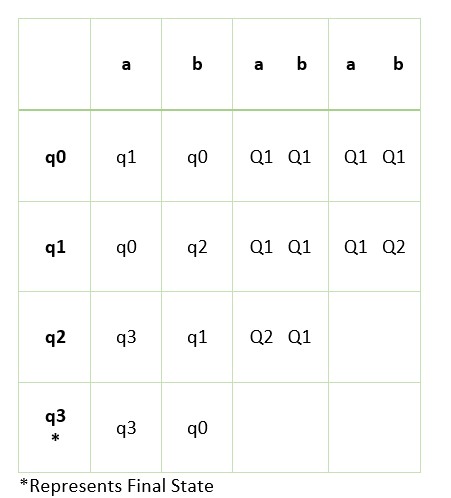
Now we identify the transition of DFA.

The below table shows the complete transition table and its movement to the sets.

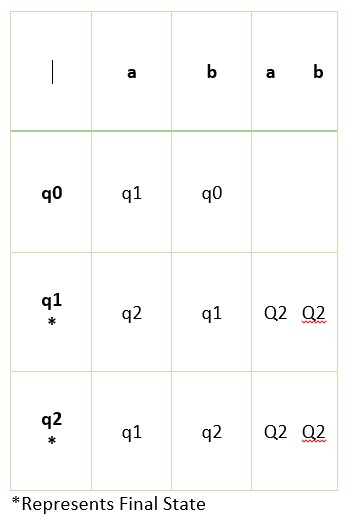
We do not consider the state q0 because we have only one state in the non-final set.

The set Q2 has two states. So check for the division of the set.

On state q1, when we apply the input symbol 0, we move to state q2.

The state q2 is in the set Q2. So we write Q2 in the fourth column.

Similarly, write the set names for all the transitions.

Take a look at the complete table. From the table, we notice state q1 and q2 are moving to the same sets.

So we stop here because the transition is repeating the same sets.

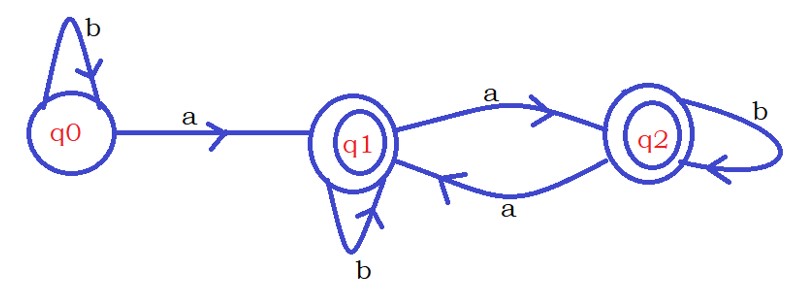
Now we can combine the states q1 and q2 because they are moving to the same sets.

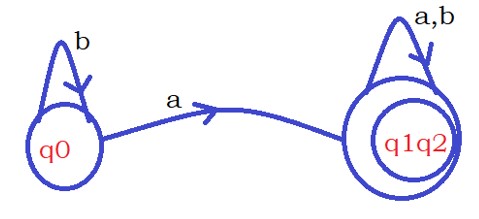
The below diagram shows the final minimized transition diagram.

Take one more example:

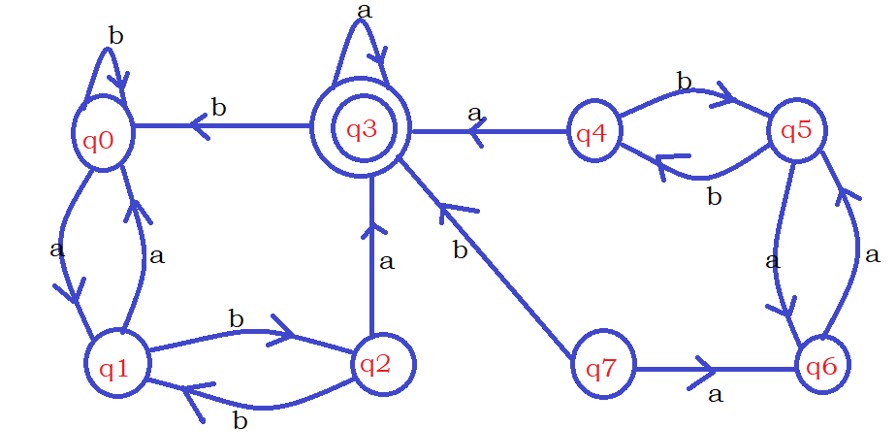
The states q4, q5, q6, and q7 are not reachable from the initial state.