NFA to DFA with Multiple Final States Example

For Complete YouTube Video: Click Here

In this class, We discuss NFA to DFA with Multiple Final States Example

The reader should have prior knowledge of NFA to DFA conversion. Click Here.

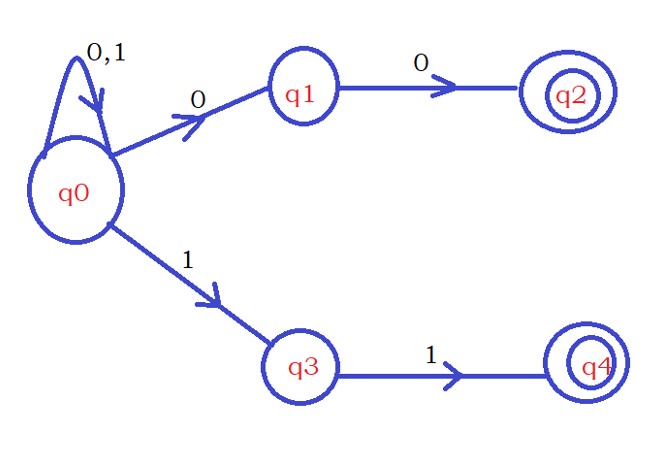
We consider the below given NFA.

First step: Write the transition table for the given NFA.

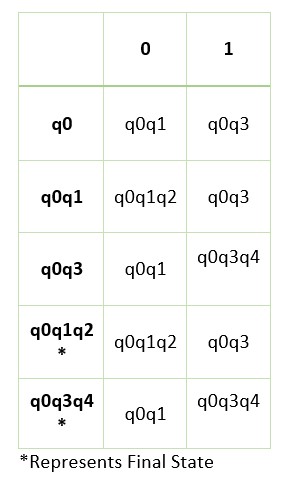
The below table shows the transition table for the NFA.

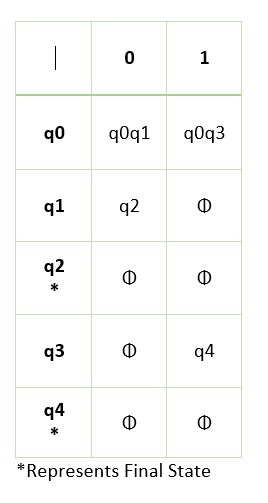
The initial state is q0, and we have two final states q2 and q4.

Conversion Procedure

First step: consider the initial state transition in the NFA. and write it in the DFA transition table.

On state q0, if we see input symbol zero, we move to q0 and q1.

On state q0, if we encounter input symbol one, we move to state q0 and q3.

Second Step: The states obtained from step one are considered.

Chose the combination of states that are not yet written transition in the DFA transition table.

From the first step, q0,q1 is the combination not yet taken as a new state.

So q0,q1 is taken as our new state in the DFA transition table.

The below example shows the transition for the new state q0,q1.

δ'((q0,q1),0) = δ((q0,q1),0)

δ((q0,q1),0) is given as δ(q0,0) ∪ δ(q1,0). ∪ represent union.

δ(q0,0) is q0,q1 from given NFA table.

δ(q1,0) is q2 from the given NFA table.

δ(q0,0) ∪ δ(q1,0) gives q0,q1,q2.

Similarly, identify transition for state q0,q1 for input character 1.

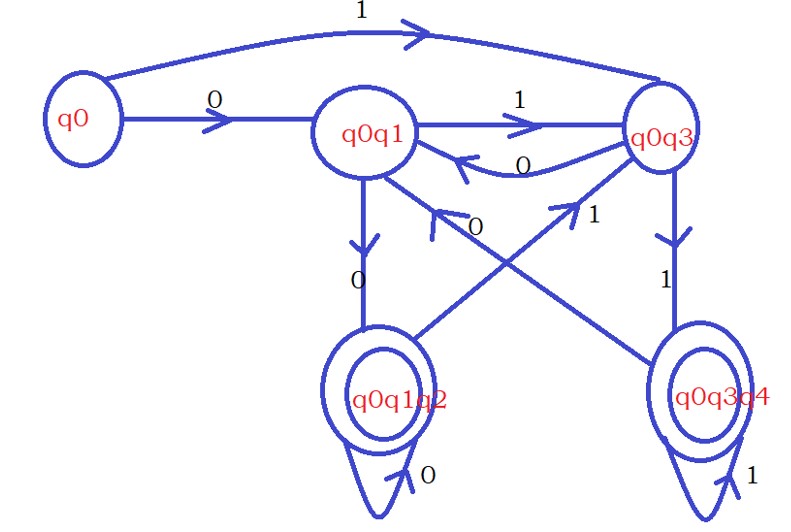
Repeat step two until no new combinations of states in the DFA transition table.

We have q2 and q4 as final states.

In the DFA transition table, whatever the states contain q2 or q4, or both. We take that state as the final state.