NFA with Epsilon Moves
For Complete YouTube Video: Click Here
In this class, we discuss NFA with Epsilon Moves.
The reader should have prior knowledge of how NFA executes. Click Here.
Let’s refresh the concept of how NFA executes, and then we go to epsilon moves.
Nondeterministic Finite Automata: We define NFA using five tuples.
M={Q,Σ,q0,F,δ}
Q is a finite set of states.
Σ is a finite set of input symbols.
q0 is the initial state.
F is a finite set of final states. In our example, we have one final state qf.
δ is the transition function. We represent transition function as δ: QXΣ->Q.
Condition 1: One input symbol causes to move more than one state.
The below diagram shows condition 1.
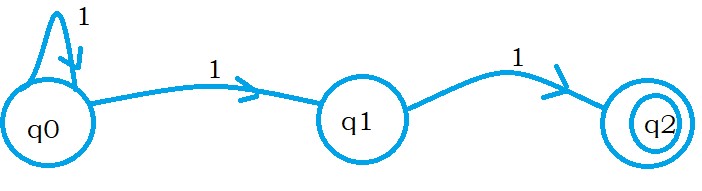
After seeing input symbol one, we move to states q0 and q1.
One machine took the next input symbol and applied it on state q0.
Another machine takes the next input symbol and applies it on state q1.
Condition 2: It is not compulsory that all the states have to consume all the input symbols.
NFA is doing parallel execution.
The same way NFA with epsilon moves is also the same as NFA but with one extra condition.
Condition 3: Epsilon Moves
We are moving on states without receiving any input symbol.
The below diagram shows the NFA with epsilon moves.
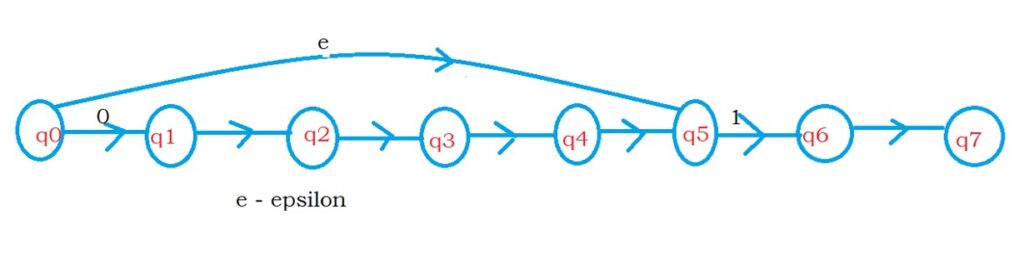
In the diagram, we are moving from state q0 to q5 using epsilon moves.
Initially, we start at state q0. Without input character, we can move to state q5.
Now, we have two machines one machine take the first input character and apply on state q0.
Another machine will take the next input and apply it on state q5.
Whats benefit do we get with these epsilon moves?
Take the input string 10001. we start applying the first input character on states q0 and q5.
The state q0 does not match the first input character, and the NFA machine will die.
Another machine applied the first input character on state q5, and it found matching and moved to the next state.
Assume we have written one logic on state q0 to q4 and another logic on state q5 to q7.
We got the flexibility to check both conditions at a time.
So writing logic in NFA with epsilon moves is easy.
The implementation of NFA with epsilon moves is also not possible in real-time. Because of parallel execution.
So write the logic in NFA with epsilon moves. Convert to NFA and then to DFA.
Conversion of NFA to DFA was discussed in our previous classes.
Next class, we discuss the conversion of NFA with epsilon moves to NFA.
Example:
Write logic to accept floating-point numbers.
The input symbols are Σ = {+,-,0-9}
Below given are examples floating-point numbers.
+20.9 is a floating-point number.
-2222.888 is a floating-point number.
2567.9 is a floating-point number.
.988 is a floating-point number.
21. is a floating-point number.
. is not a floating-point number.
From the above examples, we understand floating-point numbers start with either symbol +, – or no symbol.
Before dot no need to have digits.
After the dot symbol no need for digits.
One condition we observe we need digits on atleast one side of the dot.
The below diagram shows the NFA with epsilon moves for floating-point numbers.
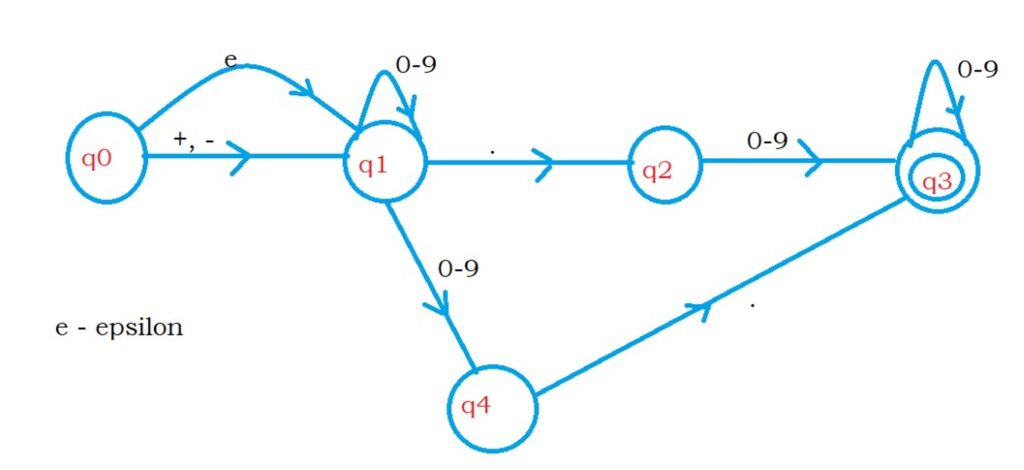
From state q0, we move to state q1 with epsilon moves.
The input symbol is applied on state q0 by one machine.
Another machine is going to apply the first input symbol on state q1.
If the first input character is + or –, one machine will move to state q1, and another will die.
Simple to write logic using NFA with epsilon moves.
On state q1, if we find the input dot, we move to state q2.
If we did not find the digit before the dot, we move to state q2, and atleast one digit should be seen to move to the final state q3.
Before dot, if we find a digit, there is no need to have a digit after dot.
This logic is taken care of in the other direction on state q1.
When we see a digit on the q1 state, we stay on q1 and move to the q4 state.
The state q4 will take the dot and move to the final state q3.
After finding the dot symbol, we may find digits or may not find digits.
On state q3, if we find any digit, we stay in the same state.
