NFA with Epsilon Moves to NFA

For Complete YouTube Video: Click Here

In this class, We discuss NFA with Epsilon Moves to NFA.

The reader should have prior knowledge of NFA with the Epsilon Moves concept. Click Here.

Example:

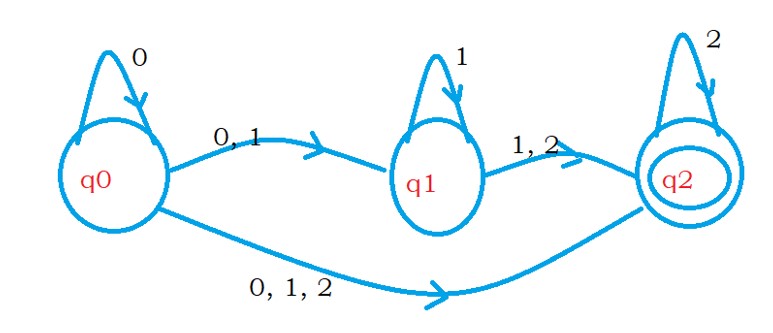
The below diagram shows the example NFA.

The diagram has epsilon moves from state q0 to q1 and from q1 to q2.

Epsilon moves help in moving from one state to another without input string.

Take input string 0.

The input symbol 0 is applied on state q0, q1, and q2.

The below equation shows the transition on state q0 on input symbol 0.

δ(q0,0) = δ(q0,0) ∪ δ(q1,0) ∪ δ(q1,0)

δ(q0,0) = q0 ∪ Φ ∪ Φ

δ(q0,0) = q0

The above equation shows how NFA with epsilon moves work.

We use δ to represent the transition on NFA with the epsilon moves diagram.

We use δ’ to represent the transition on the NFA diagram.

When we apply zero on q0, we end up in state q0.

We end up in state q0, but still, we can move from state q0 to q1 and q2 with epsilon moves.

So we write δ(q0,0) = {q0, q1, q2}.

To convert the NFA with epsilon moves to NFA without epsilon moves. First, we find the ε-closure.

ε-closure of q0 is {q0, q1, q2}. Because we move to state q1 and q2 with epsilon moves on state q0.

ε-closure(q1) = {q1, q2}.

ε-closure(q2) = {q2}

The below equation shows how to calculate transition of NFA using NFA with epsilon moves diagram.

δ'(q0, 0) = ε-closure(δ(ε-closure(q0) , 0)) 

δ'(q0, 0) = ε-closure(δ((q0, q1, q2) , 0)) because ε-closure(q0) = {q0,q1,q2}.

δ'(q0, 0) = ε-closure(δ(q0,0) ∪ δ(q1,0) ∪ δ(q2,0))

δ'(q0, 0) = ε-closure(q0 ∪ Φ ∪ Φ)

δ'(q0, 0) = ε-closure(q0)

δ'(q0, 0) = {q0,q1,q2}

The above expression shows the transition for NFA.

The below diagram shows the transition for δ'(q0, 0) = {q0,q1,q2}.

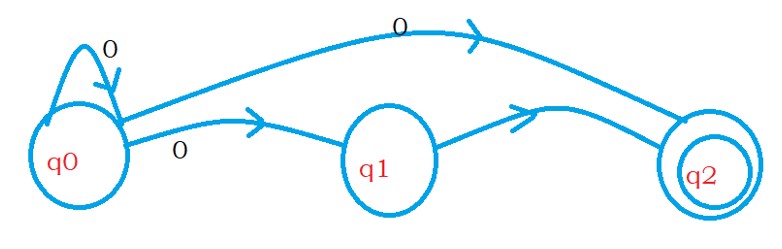
On the state q0 if we see input symbol 0 we move to state q0, q1, and q2.

After conversion to NFA we are getting the same result we got from NFA with epsilon moves.

Similarly we need to find the transition for δ'(q0, 1).

δ'(q1, 0) = ε-closure(δ(ε-closure(q1) , 1))

δ'(q0, 1) = ε-closure(δ((q0, q1, q2) , 1)) because ε-closure(q0) = {q0,q1,q2}.

δ'(q0, 1) = ε-closure(δ(q0,1) ∪ δ(q1,1) ∪ δ(q2,1))

δ'(q0, 1) = ε-closure(Φ ∪ q1 ∪ Φ)

δ'(q0, 1) = ε-closure(q1)

δ'(q0, 1) = {q1, q2}

We need to find transition for all the possible inputs and states.

δ'(q0, 2) = {q2}

δ'(q1, 0) = Φ

δ'(q1, 1) = {q1, q2}

δ'(q1, 2) = {q2}

δ'(q2, 0) = Φ

δ'(q2, 1) = Φ

δ'(q2, 2) = {q2}

The below table shows the final transition table for NFA.

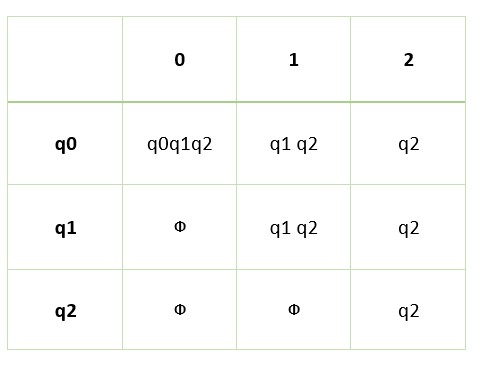
The below diagram shows the final transition diagram for NFA.