NFA with Epsilon Moves to NFA Practice Example

For Complete YouTube Video: Click Here

In this class, We discuss NFA with Epsilon Moves to NFA Practice Example.

The reader should have prior knowledge of the procedure to convert NFA with Epsilon Moves to NFA. Click Here.

Example:

Given below is an NFA with epsilon transition.

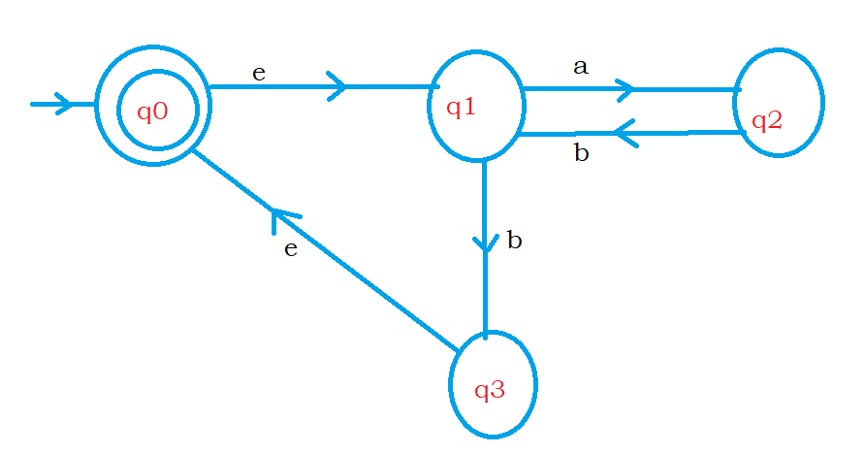
First, we have to find the epsilon closure to all the states.

ε-closure(q0) = {q0, q1}.

ε-closure(q1) = {q1}.

ε-closure(q2) = {q2}.

ε-closure(q3) = {q0, q1, q3}.

After finding the epsilon closure. We need to find the transitions of NFA using the transition of NFA with epsilon moves.

Follow the below expression to find the transition of NFA.

The intuition about the expression provided in our previous class.

δ'(q0, a) = ε-closure(δ(ε-closure(q0) , a)) 

δ'(q0, a) = ε-closure(δ((q0, q1) , a)) because ε-closure(q0) = {q0,q1}.

δ'(q0, a) = ε-closure(δ(q0,a) ∪ δ(q1,a))

δ'(q0, a) = ε-closure(Φ ∪ q2)

δ'(q0, a) = ε-closure(q2)

δ'(q0, a) = {q2}

The next transition as follows.

δ'(q0, b) = ε-closure(δ(ε-closure(q0) , b)) 

δ'(q0, b) = ε-closure(δ((q0, q1) , b)) because ε-closure(q0) = {q0,q1}.

δ'(q0, b) = ε-closure(δ(q0,b) ∪ δ(q1,b))

δ'(q0, b) = ε-closure(Φ ∪ q3)

δ'(q0, b) = ε-closure(q3)

δ'(q0, b) = {q0, q1, q3}

Similarly, The remaining transitions are done.

δ'(q1, a) = {q2}

δ'(q1, b) = {q0, q1, q3}

δ'(q2, a) = Φ

δ'(q2, b) = {q1}

δ'(q3, a) = {q2}

δ'(q3, b) = {q0, q1, q3}

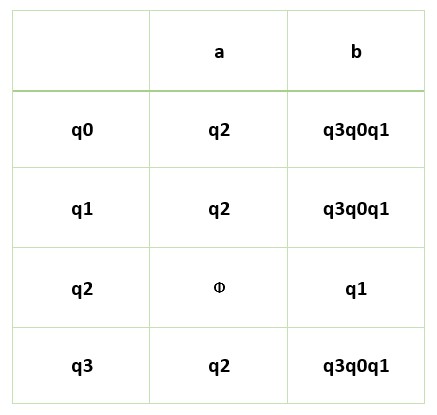
The below diagram shows the transition table for NFA.

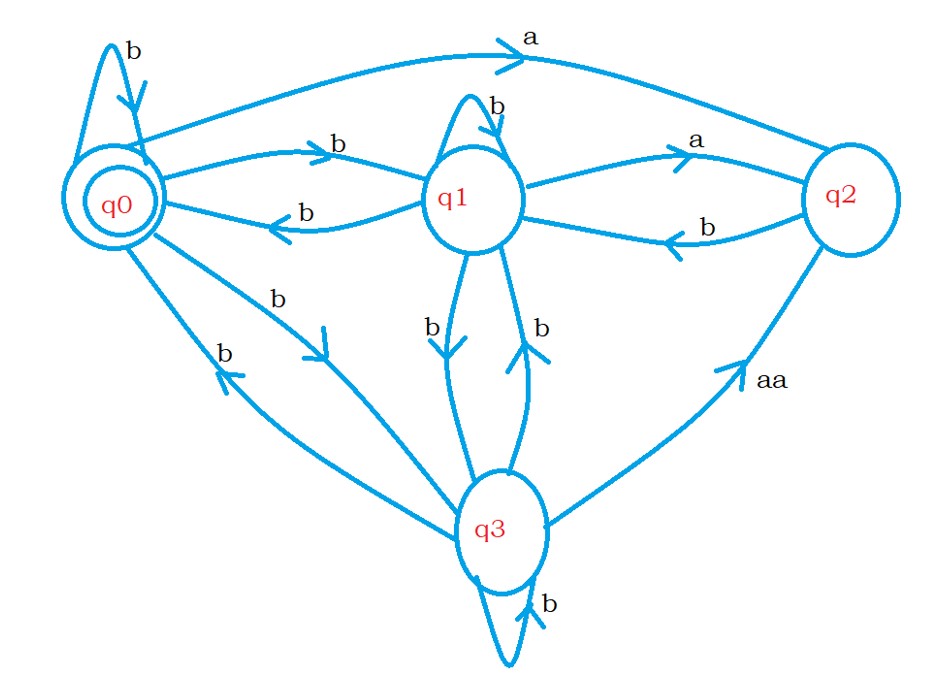
The below diagram shows the transition diagram for NFA.