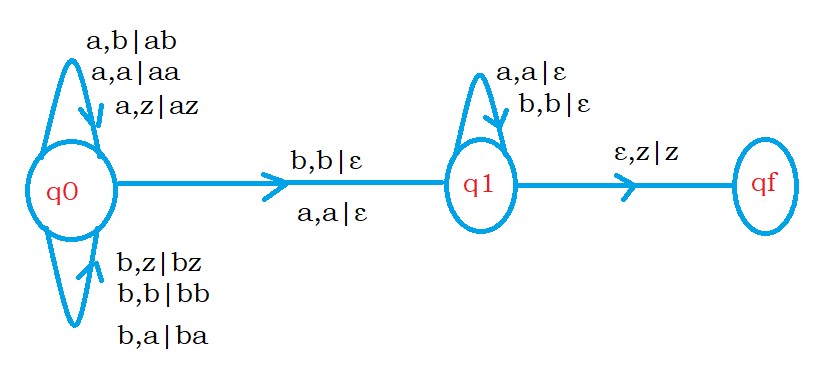
Non Deterministic PDA NDPDA

In this class, We discuss Non Deterministic PDA NDPDA.

For Complete YouTube Video: Click Here

The reader should have prior knowledge of deterministic push-down automata. Click Here.

Non Deterministic Push-Down Automata: A push-down automata is non-deterministic if one transition can take more than one move.

We can achieve NDPDA in two ways.

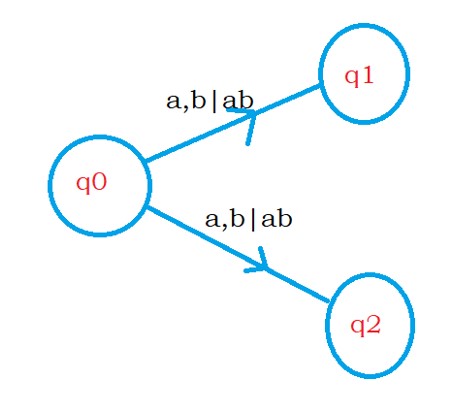
a) if two are more edges labelled with the same input and stack symbol from a state.

The below diagram shows the first case.

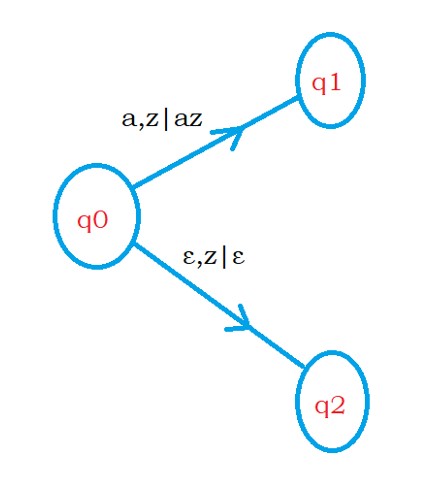
b) When a state has two edges with the same stack symbol and one input symbol is epsilon.

The below diagram shows the second case.

Now we design a few examples using non-deterministic push-down automata.

Example 1: Take the language L1 = {ww^R where w is (a,b)*} string length greater than zero.

The strings in the language L1 = {abba, abbbba, . . .}

The logic is a bit complex to understand. The reader should focus here.

The reader should have an understanding of NFA. Click Here.

Take the input string abbbba.

The first symbol is a. We push onto the stack.

The second input symbol is b. Now we need to check in two ways.

From the middle of the input string, we need to check the reverse of the string.

The confusion here is how to identify the middle of the string?

So we assume every input symbol from the second position as the middle of the string and proceed with pop operation logic.

The second logic is to assume the input symbol is not the middle of the string and go with push logic.

From the idea of nondeterminism. one PDA will move forward and check the pop operation logic.

The other PDA will stay in the same state and apply push operation logic.

During the end of the input string, one of the PDAs will succeed.

We apply NDPDA the way mentioned above.

The below diagram shows the complete NDPDA for the language L1.