Nondeterministic Finite Automata
For Complete YouTube Video: Click Here
In this class, We discuss Nondeterministic Finite Automata.
The reader should have prior knowledge of Deterministic Finite Automata. Click here.
Nondeterministic Finite Automata: We define NFA using 5 tuples.
M={Q,Σ,q0,F,δ}
Q is a finite set of states.
Σ is a finite set of input symbols.
q0 is the initial state.
F is a finite set of final states. In our example, we have one final state qf.
δ is the transition function. We represent transition function as δ: QXΣ->Q.
Condition 1: One input symbol causes to move more than one state.
The below diagram shows condition 1.
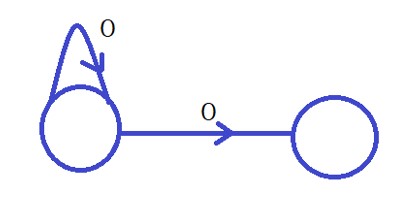
Condition 2: It is not compulsory that all the states have to consume all the input symbols.
The below diagram shows condition 2.
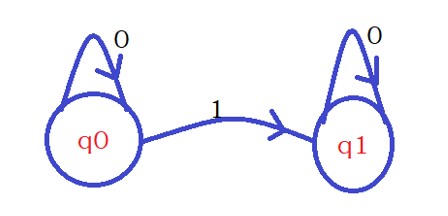
We take an example and understand how NFA executes.
With the understanding of NFA execution, we get an intuition to design NFA.
Acceptance of NFA
Example: Design NFA that accepts strings having the last two characters should be ones.
The input symbols are Σ={0,1}.
The below diagram shows the NFA accepting strings having the last two characters should be ones.
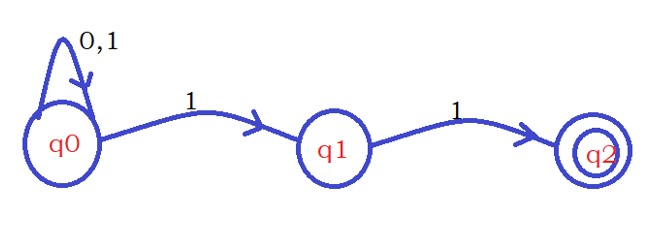
How we designed the NFA?
The reader will get clarity at the end of the class. First, we understand how NFA executes.
Example input string: 110011
Understand execution of NFA step by step.
First input character: 1
On the state q0, if we see the input character 1, we go to state q0 and q1.
We are moving to two states. So the second input character is applied on states q0 and q1.
How do we apply the second input character to two states?
We take two NFA machines. one machine will take the second input in state q0. Another machine will take the second input on state q1.
The below diagram shows the two machines.
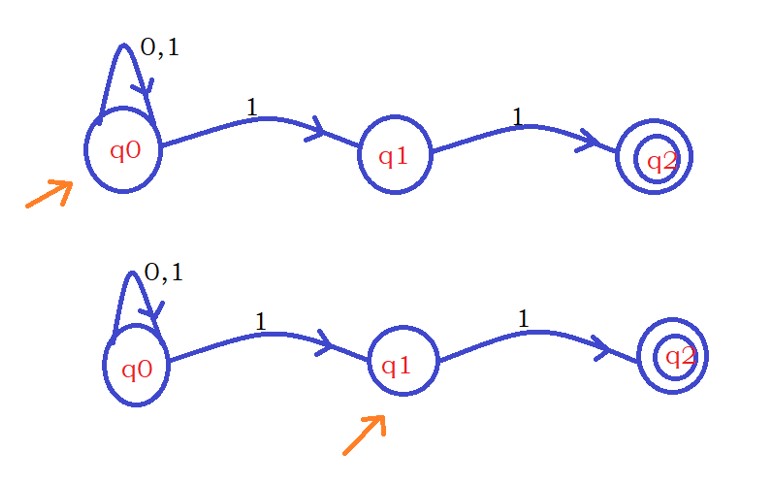
What do we need to understand from the above two machines?
One machine is going to check the base logic from the beginning taking the second input character.
Another machine is going to check the base logic, moving one step forward.
Here base logic is identifying two consecutive ones and moving to the final state.
Second Input Character: 1
The second input character is applied to the above two machines.
The first machine is again moving to states q0 and q1. For the third input character, two machines again.
The second machine moves to state q2.
Total three machines for third input character.
The below diagram shows the three machines.
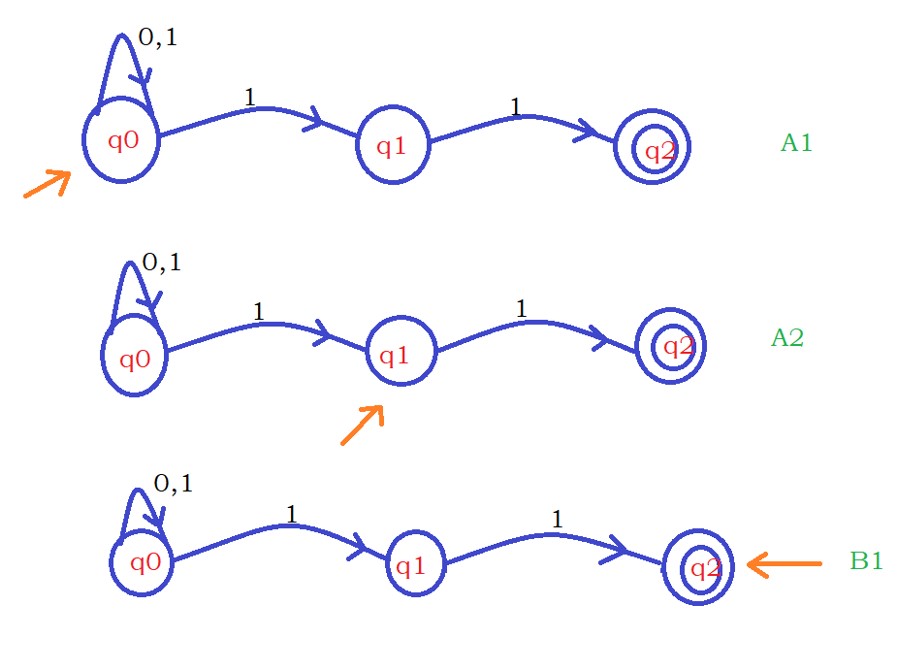
One machine takes the third input on state q0.
The second machine takes the third input on state q1.
The third machine takes the third input on state q2.
What do we understand from the above machines?
One machine takes the third input character and checks the base logic from starting.
Another machine takes the third input character and checks the base logic considering the previous one character.
The third machine takes the third input character and checks the base logic considering the previous two input characters.
Third Input character: 0
The third input character is applied on the above three machines.
The first machine takes input on state q0 and moves to state q0.
The second machine takes input on state q1 and dead because of no transition about input zero on state q1.
The third machine takes input on state q2 and dead because of no transition about input zero on state q2.
For the fourth input character, we remain with one machine.
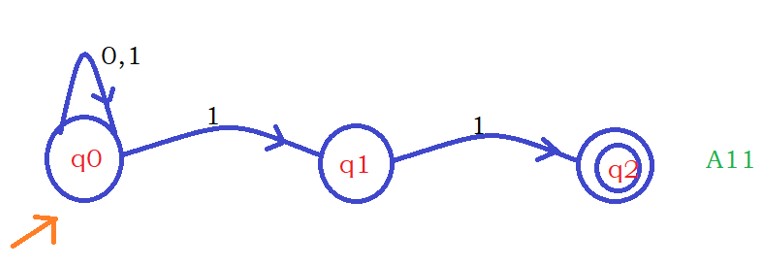
Fourth input character: 0
The fourth input is given to the above machine.
The machine takes input on state q0 and moves to state q0.
The below diagram shows the NFA.

Fifth input character: 1
On applying the fifth input, we get two machines.
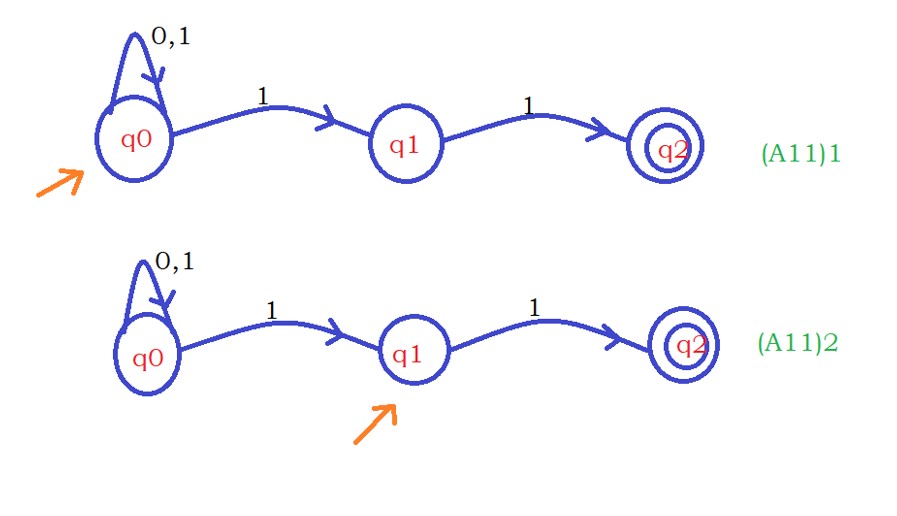
One will take the sixth input on state q0.
Another will take the sixth input on state q1.
Similar to the first input character.
Sixth input character: 1
Applying the sixth input character on the above two machines, we get three machines.
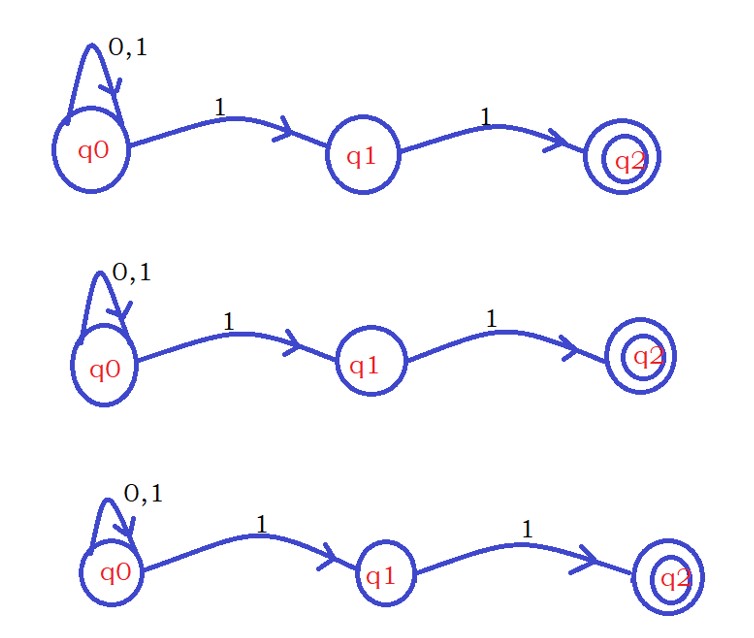
Similar to the second input character.
One machine takes the seventh input character on state q0.
The second will take the seventh input on state q1.
The third machine will take the seventh input on state q2.
But we do not have a seventh input character.
After completing the input string, if any of the machines is in the final state, the string is accepted. Otherwise not accepted.
Our input string is accepted because the third machine is in state q2.
NFA will take parallel execution; it is not possible in real-time.
Understand in a known way.
Assume each machine is a processor.
Parallel implementation of logic on different processors is not possible in real-time. Because based on the input, we may need two or three processors.
We do not know how many processors are needed in advance.
Writing logic in NFA is easy, but implementation is not possible.
So we need to convert NFA to DFA for implementation.
We discuss the conversion of NFA to DFA in our later classes.
