Pumping Lemma for Regular Languages

For Complete YouTube Video: Click Here

In this class, We discuss Pumping Lemma for Regular Languages.

The reader should have prior knowledge of finite automata and regular expressions. Click here.

We will refresh the concept required to understand this class. Then we go to pumping lemma.

Take a language L1 = {1, 01, 11}

The language L1 is a finite language because L1 has a finite set of strings.

Any finite language is a regular language.

Take the language L2 = {abb, ababb, abababb, . . .}

The language L2 is infinite language. It has an infinite number of strings.

The language l2 accepts strings start with a and end with bb. In between, we can have any number of ba.

The below diagram shows the finite automata for the language L2.

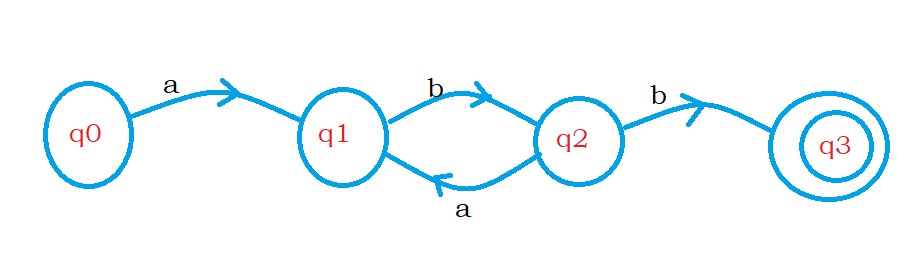
In the above finite automata on states q1 and q2, we are repeating the pattern ba.

In regular expressions, we write the repetition of ba. as (ba)*.

We have this star operator to write the regular expressions for infinite language.

We find a pattern to repeat using the star operator.

Now we get an idea about pumping lemma.

We take any string from the given language.

For example, we consider the string ababb.

We separate the string into three parts as a (ba) bb.

We keep pumping the string

a (ba)ⁱ bb

If i = 0, we get the string abb

if i = 1, we get the string ababb.

If i = 2, we get the string abababb.

As we take different i values, we are generating the strings in the language.

Take one more example.

The below finite automata show an example from finite automata to regular expression using state elimination.

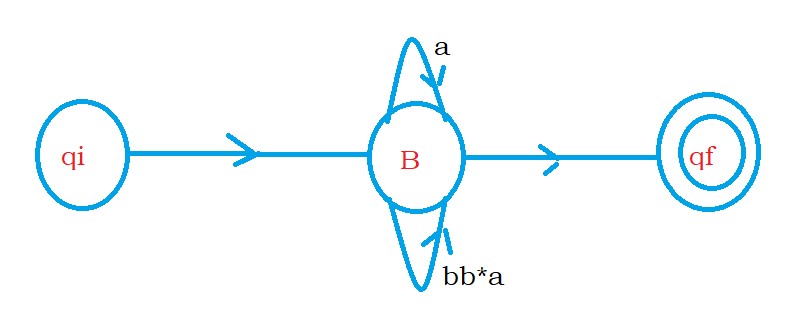
On state B, we can take a or bb*a any number of times. (a+bb*a)*.

Point to understand: we are repeating a pattern.

Pumping Lemma: The pumping lemma is used to prove a language is not regular.

Take a language L3 = { ε, ab, aabb, aaabbb, . . .}

L3 = aⁿbⁿ where n >=0

We discussed previous class the language L3 is not a regular language.

Now we prove that the language is not regular using pumping lemma.

Take any string from the given language. We are taking aabb.

We divide the string into three parts x, y, z. where y should not be epsilon.

Example 1: x = ε, y = aabb, z = ε

we write as x(y)ⁱz

ε(aabb)ⁱε we keep on pumping y.

i = 1 we get aabb

i =2 we get aabbaabb this string is not belong to language L3.

We try for another pattern.

Example 2: x = a y = ab z = b

we write as x(y)ⁱz

a(ab)ⁱb we keep on pumping y.

i =1 we get aabb

i = 2 we get aababb. the string is not in the given language.

If we show no pattern generates the strings present in our language, we say the language is not regular.