Regular Expression to Finite Automata Closure

For Complete YouTube Video: Click Here

In this class, We discuss Regular Expression to Finite Automata Closure.

The reader should have prior knowledge of NFA with epsilon moves and regular expression to finite automata union. Click Here.

Understanding this class is very important please read the class till the end. The last example is important to understand.

Take examples and understand how we construct finite automata from the regular expression.

Example: Below given regular expression over the alphabet Σ = {0,1}.

A regular expression is 1*.

The language for the regular expression 1* is {ε, 1, 11, . . . . }.

The below diagram shows equivalent NFA for regular expression 1*.

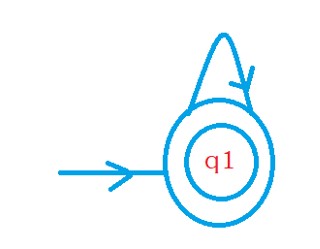
The NFA has one state, q1. The state q1 is the initial state and final state.

On state q1, if we see input symbol one, we move to state q1.

The NFA will accept zero ones, single ones, two ones, so on.

The below diagram shows the equivalent NFA with epsilon moves to regular expression 1*.

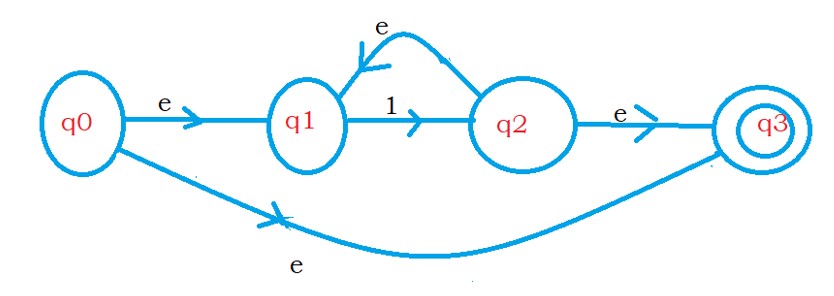
For better understanding, we are showing both NFA and NFA with epsilon moves.

The above NFA with epsilon moves will accept epsilon and any number of ones.

Example 2: The given regular expression (11)*.

The language generated by the regular expression (11)* is {ε, 11, 1111, . . . .}.

The language contains an even number of ones.

The below diagram shows NFA with epsilon moves to the regular expression (11)*.

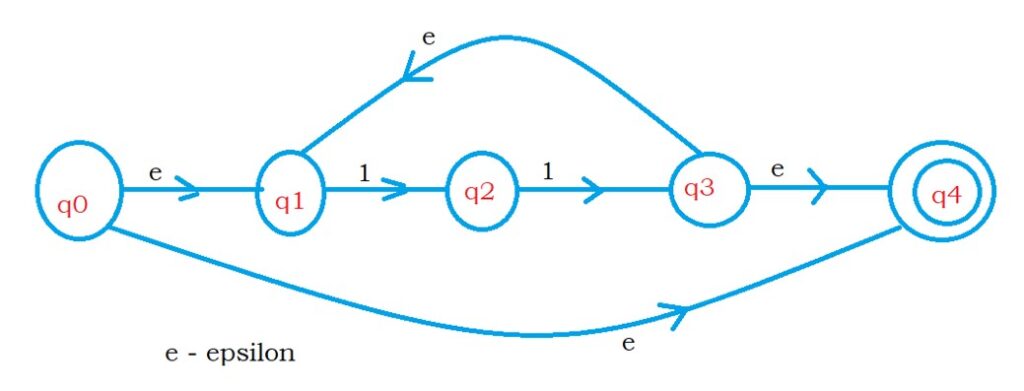
Point to understand: On state q0, we are moving to the final state with epsilon moves.

We use the above point to accept the string epsilon.

Next point to understand: On state q3, we are moving back to state q1 with epsilon moves to check logic 11.

The above two points help the reader construct NFA with epsilon moves to any regular expression with closure property.

Example 3: The given regular expression is (0+1)*.

The language generated by the regular expression is {ε, 0, 1, 01, 10, 11, . . . }

Any string generated using the alphabet {0,1} is accepted in the language.

The below NFA with epsilon moves is equivalent to regular expression (0 + 1)*.

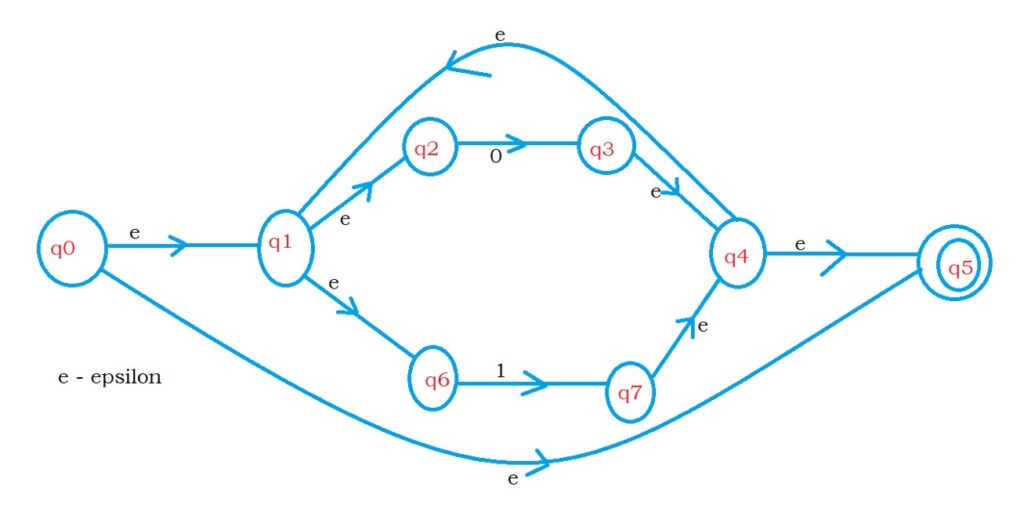
We explained how to construct NFA for (0 + 1).

We need to repeat the logic of (0 + 1) any number of times.

The logic to repeat is explained above in example 2.

On state q0, we are moving to state q5 with epsilon moves to accept epsilon.

On state q4, we are moving to state q1 with epsilon moves to repeat the logic (0 + 1).

Example 4: The given regular expression (0 + 1)* 11.

Divide the expression into two parts.

One part is (0 + 1)*, and the other part is 11.

The first part is accepting strings generated by the alphabet {0,1}.

We concatenate 11 to the first part.

We discussed how to draw NFA for the concatenation operator.

The language generated by the regular expression (0 + 1)* 11 is {11, 011, 111, 0111, . . . }

The language says the last two input characters should be 11.

The below diagram shows the NFA with epsilon moves to the regular expression (0 + 1)* 11.

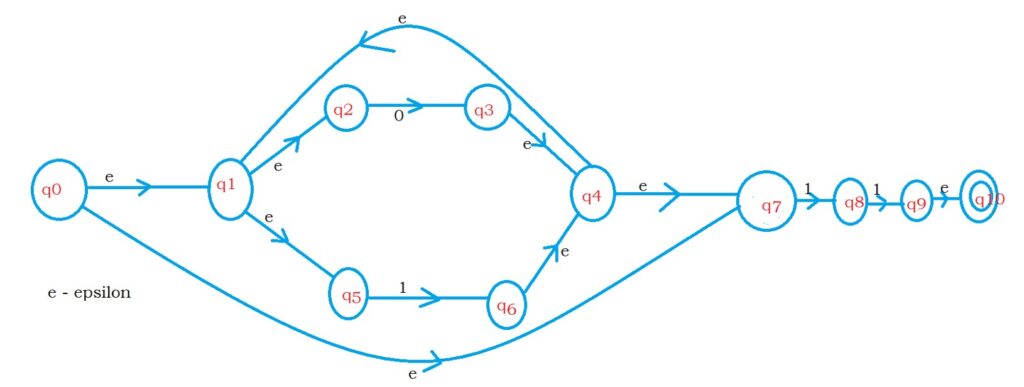
Up to state q7, the NFA shows logic to the regular expression (0 + 1)*.

After q7, the NFA is showing logic to accept 11.

We concatenate Both NFA’s, so place epsilon between two NFAs.

Point to understand: How the above NFA is executing to accept the strings containing the last two characters 11.

Take some examples and understand how NFA is executing.

Example: take input string 11.

On state q0, we are moving to state q7 with epsilon moves. One machine checks logic 11, and the other checks logic (0 + 1)*.

After seeing input 11, one of the machines moved to the final state. So accepted.

Example: take the input string 0111.

After seeing the first input character 0, we are moving to state q7.

From q7, we are moving to state q1.

So one NFA is checking logic 11, and another machine is going back to check the logic (0 + 1)*.

So whenever we see the last two characters 11. one of the machines will move to the final state.