Regular Expression to Finite Automata Union and Concatenation

For Complete YouTube Video: Click Here

In this class, We discuss Regular Expression to Finite Automata Union and Concatenation.

The reader should have prior knowledge of regular expression operators. Click Here.

We convert the regular expression to NFA with epsilon moves. Would you please read our NFA with epsilon moves class for better understanding?

Example 1:

Take a language L1.

L1 = {1}.

The regular expression for the language L1 is 1.

We write the expression as 1.

Example 2:

Take a language L2.

L2 = {11}.

The language L2 consists of string 11.

the input symbol one followed by another input symbol one.

Here in this language, the concatenation operator will satisfy.

The regular expression is written as 1.1 or simply 11.

Equivalence of Regular expression to finite automata for concatenation.

The below finite automata show the equivalent finite automata for the language L2.

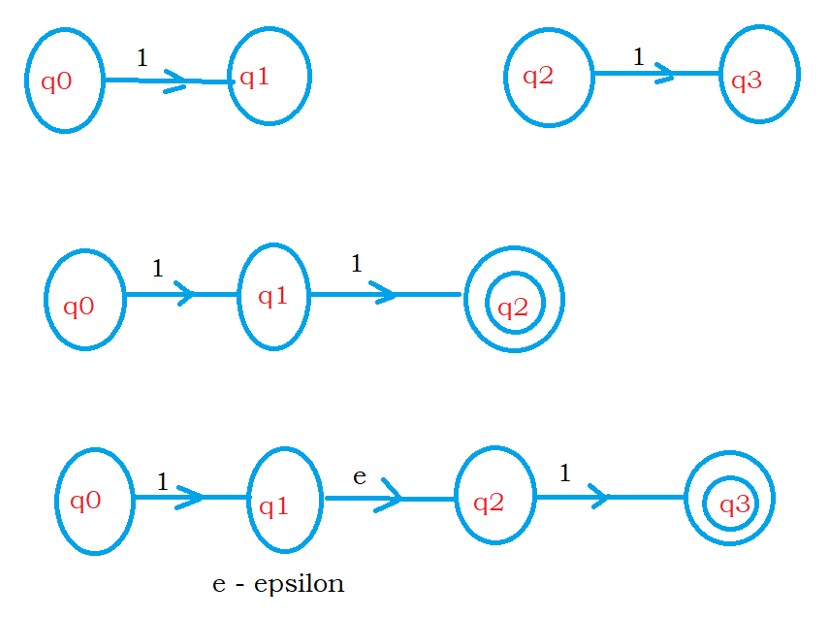
The above diagram first line first diagram shows finite automata to accept 1.

After accepting one, we need to take one more one. So the first line second diagram accepts the second one.

The second diagram shows the acceptance of two ones using NFA.

For concatenation, join the two finite automata.

The third diagram shows the acceptance of two ones using NFA with epsilon moves.

For better understanding, we are showing both NFA and NFA with epsilon moves example.

Point to Understand: We need to write finite automata for the concatenation operator, as explained below.

Assume accepting one is first logic. And taking one more one is second logic.

First logic followed by second logic is given as first NFA followed by second NFA. In between, write an epsilon move.

One more Example: The given language L3 = {110}.

The regular expression for the language is 1.1.0 or 110.

The below diagram shows the NFA with epsilon moves for the regular expression 1.1.0

Example on Union Operator:

Take a language L1.

L1 is a set of strings containing either 11 or 00.

L1 = { 11, 00}.

The regular expression for language L1 is (1.1) + (0.0).

We use the symbol plus to represent the union operator.

The regular expression to identify 11 is 1.1

The regular expression to identify 00 is 0.0

The regular expression to identify either 11 or 00 is given using the union operator as (1.1) + (0.0).

The below NFA shows the example to identify the language L1.

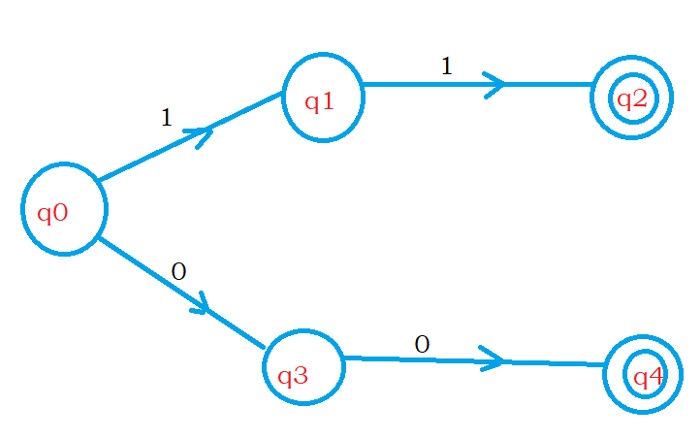
Whenever we have a union operator, we have two options at state q0.

The finite automata can find any one of the strings and move to the final state

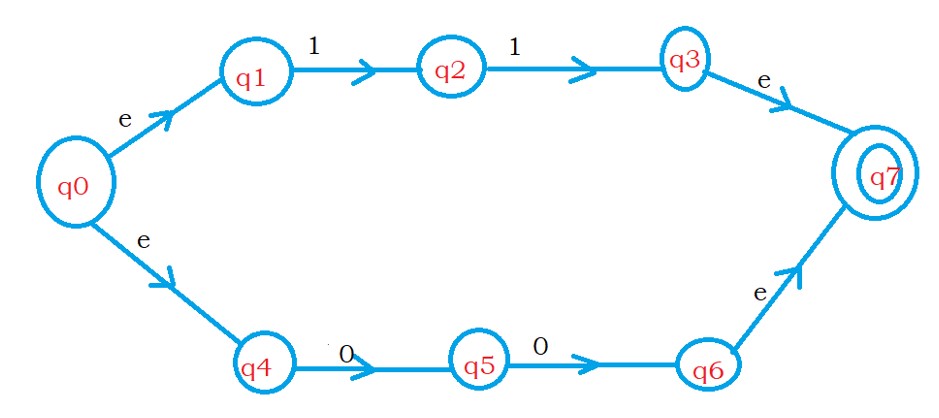
The below diagram shows the NFA with epsilon moves for regular expression (1.1) + (0.0).

In our next class, we discuss how to write finite automata for closure operators. It is essential to understand.

With the understanding of the closure operator, one can quickly write regular expressions for a given language.