Regular Language Closure Properties

For Complete YouTube Video: Click Here

In this class, We discuss Regular Language Closure Properties.

The reader should have prior knowledge of regular expressions. Click Here.

Regular Language: A language is said to be regular if we can construct finite automata or regular expression.

Example:

L1 set of strings contain the last two characters aa.

L2 set of strings contains aa as a substring.

L3 set of strings of the form aⁿbⁿ where n >= 0.

The language L3 is not a regular language. Reason explained in our previous class. Click Here.

Closure Properties of Regular Languages:

a) The union of two regular languages is regular.

Closure Properties means to take one regular language and take another regular language. Union of the two regular languages should also be regular.

The closure property satisfies the union. So we say regular languages are closed under union.

Example: Take two languages.

L1 = 01*

L2 = 11

L1 ∪ L2 can be written as 01* + 11.

Using the plus operator, we can write a union of two regular expressions.

b) The complement of a regular language is regular.

Example:

Take a language L = { set of all strings containing the last two characters aa}

The below diagram shows the finite automata for the language L.

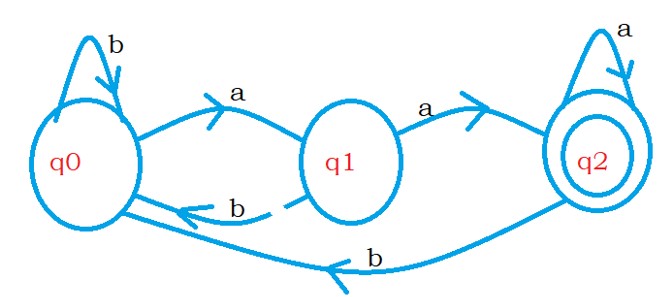
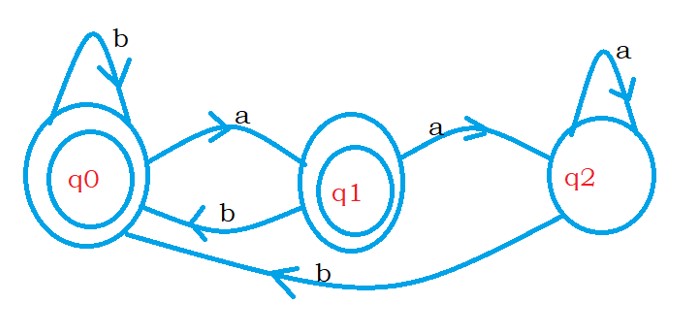
The complement of the language L’ = {set of strings not containing last two characters aa}

We get the finite automata for language L’ by changing the final states to non-final and non-final states to final.

The below diagram shows the finite automata for language L’.

c) The intersection of two regular languages is regular.

The above example shows the complement of a regular language is regular.

Example: Take two regular languages, L and M.

L ∩ M is written as (L’ ∪ M’)’.

As discussed, union and complement are closed, and we say the intersection is closed.

We write the intersection using complement and union.

d) The difference between two regular languages is regular.

Example: Take two languages, L and M.

L – M is given as L ∩ M’.

As we already discussed, the intersection and complement are closed. So the difference is closed.

We write the difference can using intersection and complement.

e) The reverse of a regular language is regular.

Understand what the reverse of a language is.

Example: Take a language L = set of strings containing the last two characters as aa.

L = { aa, baa, abaa, . . .}

The reverse of the language L^r = {aa,aab, aaba, . . .}

Take the string from language L and reverse the string.

We will show the proof in the next class. Click Here.

f) The closure of a regular language is regular.

Closure means star operator.

Example: Take a language L = (0 + 1)

L* is given as (0 + 1)*.

Adding star operator ta a regular expression, we get a regular expression.

We say the closure of a regular language is regular.

g) The concatenation of a regular language is regular.

Example:

Take an example L = (0 + 1) and M = 1*.

Concatenation of two regular expressions we get (0 + 1)1*.

We say concatenation of a regular language is regular.

h) Homomorphism or Substitution

The homorphism of a regular language is regular.

Example: Take a language L = 01* + 10*

h(0) means homomorphism of 0 is given ab.

h(0) = ab. In place of 0 substitute ab.

Similarly, h(1) = ε

On substituting ab and epsilon in the expression 01* + 10*. We get a regular expression.

abε* + ε(ab)*

ab + (ab)*

(ab)*

h) Inverse homomorphism of a regular language is also regular.

Example: Take a language L = { aa, aabb, baab, ababa}

h(0) = aa and h(1) = bb

Inverse homomorphism means substitute 0 in place of aa and 1 in place of bb.

We get the language h'(L) = {0,01}.

We can not convert the third-string in the language L, so we leave the string.

We are not going into proof of inverse homomorphism.