Reverse of a Regular Language

For Complete YouTube Video: Click Here

In this class, we discuss the Reverse of a Regular Language.

The reader should have prior knowledge of Finite automata. Click Here.

Take some examples and understand the reverse of a regular language.

Example 1:

L = { set of strings start with a over the alphabet Σ {a,b}.

L = { 10, 110, 1010 . . . }

L reverse = { 01, 011, 0101, . . .}

We reverse the strings in the language.

L reverse is the strings that end with one.

The below diagram shows the DFA for the language L.

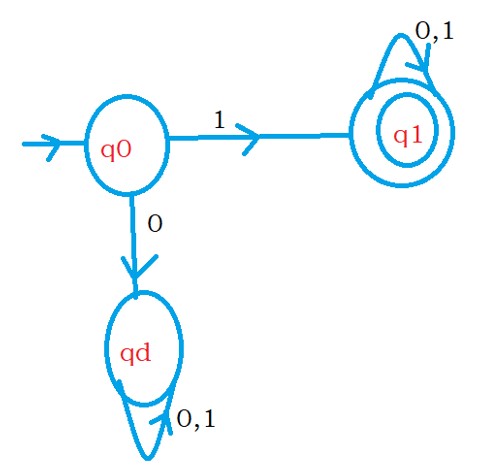
To construct the finite automata for L reverse. Change initial state as the final state and the final state as the initial state.

After changing states, reverse the arrows.

The below diagram shows the finite automata for language L reverse.

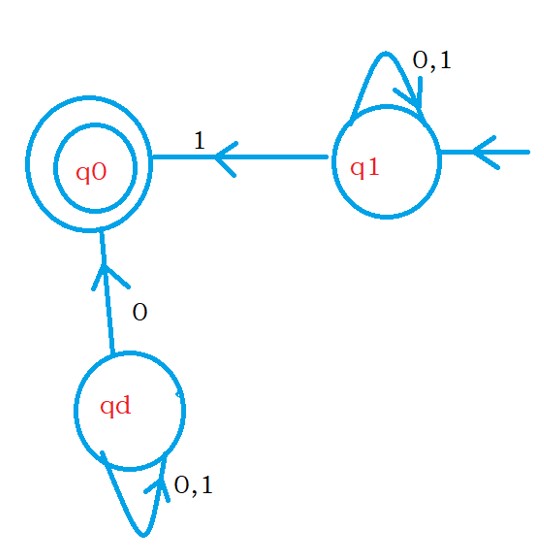
Example 2:

L2 = { set of strings contain aa as sub string}

The below diagram shows the DFA for the language L2.

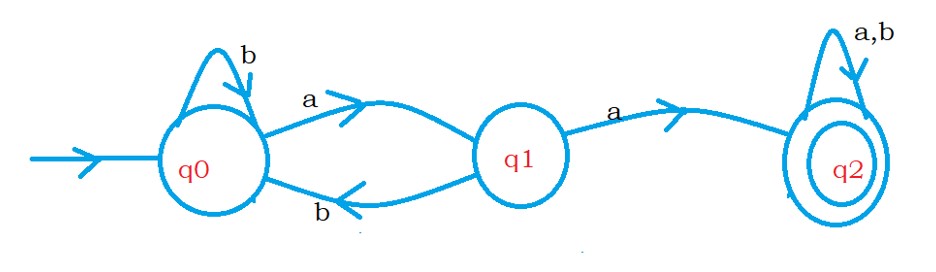
Change initial state to final state and final state to initial state.

After changing states, reverse the arrows.

The below diagram shows the finite automata for language L2 reverse.

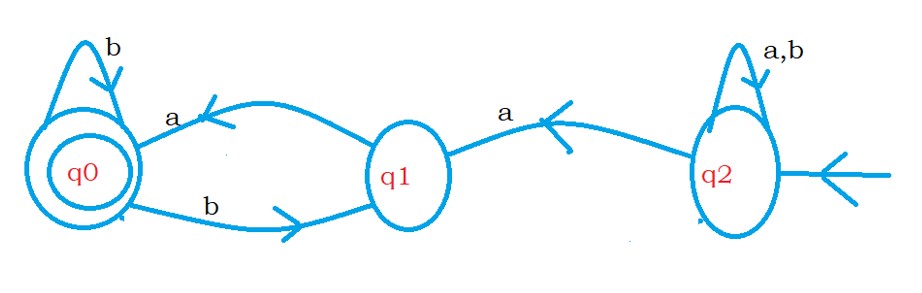
Example 3: Finite automata with multiple final states.

When we reverse the finite automata with multiple final states, we must convert to the single final state.

L3 = { set of string not containing last two characters as 11.

The below diagram shows the set of strings not containing the last two characters as 11.

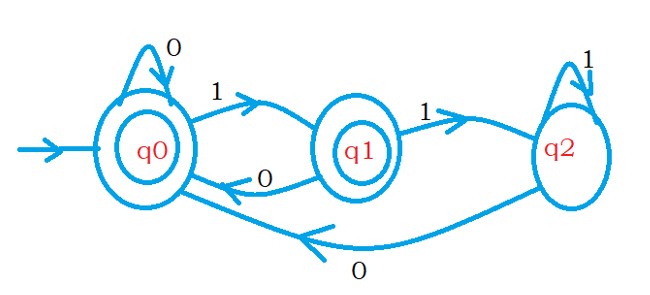
L3reverse is a set of strings not containing the first two characters as 11.

When we have multiple final states, make final states as nonfinal states.

Add a new final state and move to the final state using epsilon

The below diagram shows the finite automata after adding a new final state.

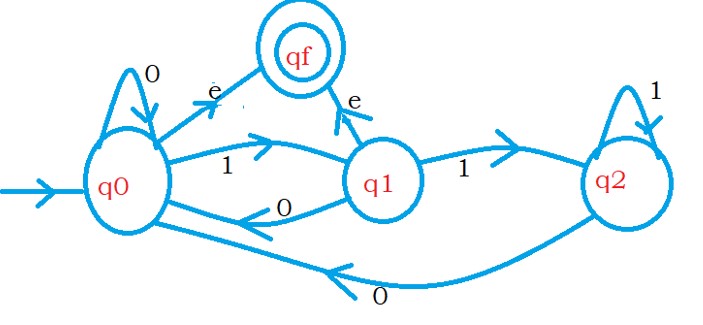
Now we have to make the initial as final state and the final state as initial.

We need to reverse the arrows.

The below diagram shows the finite automata after reversing the arrows.

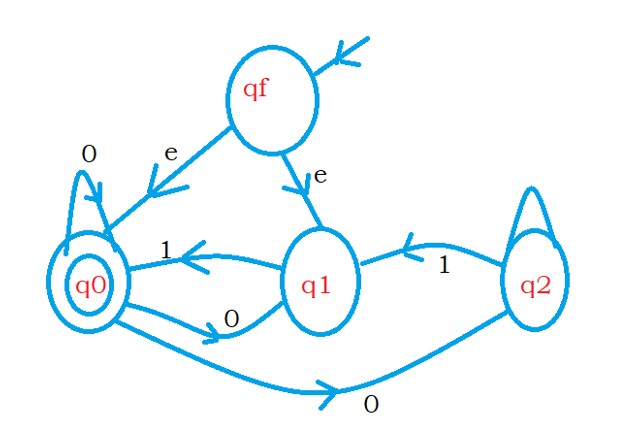
The final finite automata have epsilon moves.

The final automata do not accept the strings containing the first two characters 11.