Right and Left Linear Grammar Acceptance of Strings
For Complete YouTube Video: Click Here
In this class, We discuss Right and Left Linear Grammar Acceptance of Strings.
The reader should have prior knowledge of right and left linear grammar. Click Here.
The intuition to understand the acceptance of string by grammar was provided in the previous class.
Example 1:
Take a language L = set of strings not containing the last two characters as 11.
The below grammar accepts strings that do not contain the last two characters as 11.
q0 – 0q0 | 1q1 | 0 | 1
q1 – 0q0 |1q2 | 0
q2 – 0q0 | 1q2 | 0
The above grammar follows the right linear grammar conditions.
How to write grammar is explained in our next classes.
Input string 0101.
The above grammar has to accept the string 0101. the last two characters are not 11.
We start from the initial state q0.
The state q0 has two options by taking input character 0.
It can stop, or it can call q0.
We are choosing 0q0 production based on the input string.
The below diagram shows the complete processing of the string 0101.
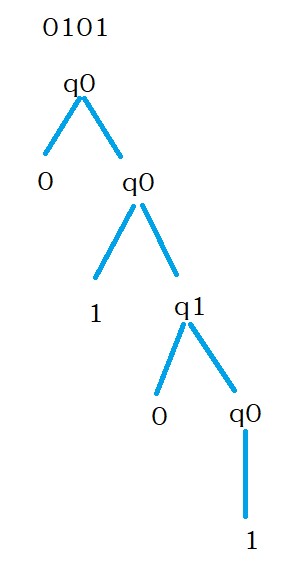
The string is accepted.
Take, an example, input string 0111.
The string is not accepted because the last two characters are 11.
The below diagram shows the complete processing of string 0111.
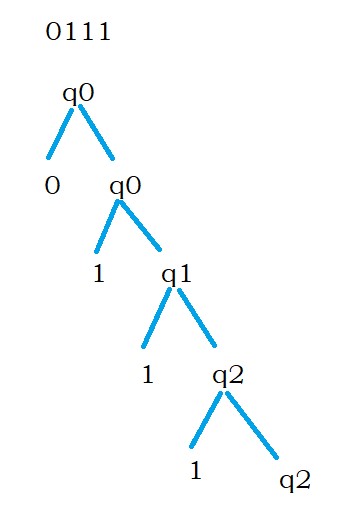
We are unable to process using the given grammar.
The string is not accepted.
Example 2: Left Linear grammar.
Take language L = set of strings to start with a.
The below grammar is left linear grammar to accept a set of strings starting with a.
B – Ba | Bb |Aa
A – ε
Take the input string aba.
The below is the complete processing to accept the string aba.
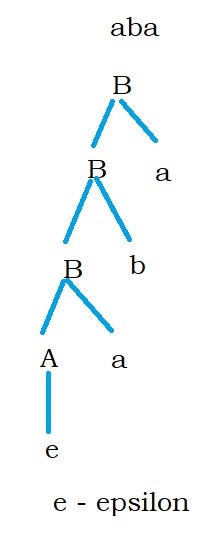
We chose first B – Ba.
The nonterminal is on the left side of the production.
So identify logic from the end of the string to start.
The end character is zero, so we have chosen B – B0.
Similarly, move on. The string is accepted.
Take another input string bba.
The below is the final diagram to process the string bba.
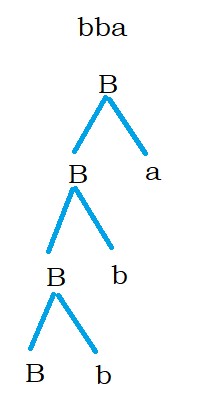
We are unable to process the string bba. The string is not accepted.
