Turing Machine as Adder

In this class, We discuss Turing Machine as Adder.

For Complete YouTube Video: Click Here

The reader should have prior knowledge of constructing the Turing machine. Click Here.

We can use the Turing machine for adding two numbers, and in our example, we use unary numbers.

First, we understand unary numbers.

We write the Decimal value five as five zeros in the unary number system.

X = 5 written as 00000

Similarly, Y = 6 is written as six zeros 000000.

The below diagram shows the storage of unary numbers in the tape memory.

Decimal value five showed as five zero’s.

Decimal value six showed as six zero’s.

To separate the two numbers, we use the symbol X.

When we add five and six, we get 11.

Decimal value eleven showed as eleven zero’s

Logic:

The turing machine starts at the start of the input.

We move right till we find ‘X.’

We covert the symbol ‘X’ to zero.

Now on the tape, we have 12 zeros.

We need to change one zero to a blank symbol.

We move to the end of the input till we find a blank.

We convert the last zero to blank.

We remain with eleven zeros.

The below diagram shows the Turing machine for addition.

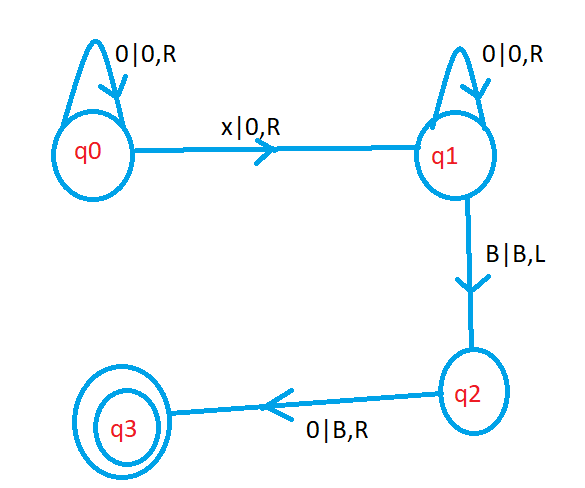
The state q0 used to move till we find ‘X.’

On state q0, if we see input symbol 0, we move right.

On the state q0, if we see the input symbol ‘X,’ we change to zero and move right and move to state q1.

The state q1 is used to move the end of the second input.

On state q1, if we see input symbol 0, we move right till we find a blank.

On state q1, if we see the input symbol ‘B,’ we move left and move to state q2.

On state q2, if we see the input symbol zero, we convert to zero and move to halt state.