Understanding Push Down Automata
In this class, We discuss Understanding Push Down Automata.
For Complete YouTube Video: Click Here
The reader should have prior knowledge of context-free grammar and languages. Click Here.
Push Down Automata (PDA): One way to represent context-free languages.
Push-down automata are similar to finite automata with extra stack memory, and we can do three operations on the stack memory.
Push operation
pop, and no operation.
Example: Take an example language L = {aⁿbⁿ where n >= 1}
The below diagram shows the push-down automata for the language L.
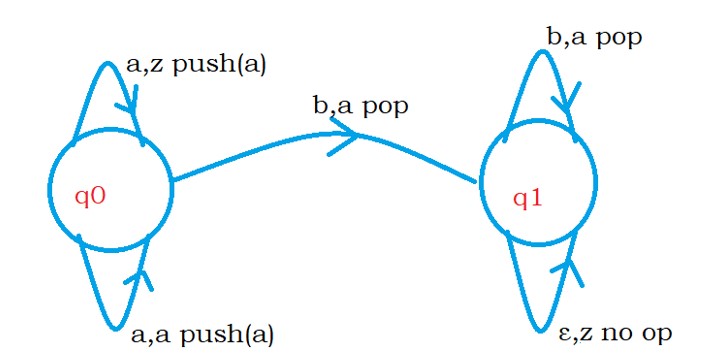
Here we need to count the number of a’s.
We count the number of a’s using the stack memory.
The symbol z is the starting symbol in the stack.
The symbol z shows the stack is empty.
The intuition to the push-down automata is provided using input string aaabbb.
The input string aaabbb belongs to the language L.
Whenever we see the input symbol a, we push on to the stack.
After observing the first b in the input string, we need to pop from the stack.
For each b, pop an element from the stack.
When the input string is completed, if the stack is empty. We found an equal number of b’s.
Now we understand the complete diagram.
The state q0 is our starting state.
On the state q0, if we found input symbol a and the stack top symbol is z, we need to push ‘a’ onto the stack.
On the state q0. If the input symbol is a and the stack top symbol is a. we need to push symbol a to the stack.
After seeing the first input symbol b., we change to state q1.
We need to change our logic from now.
On state q0, if we see input symbol b and stack top is a, we need to pop an element from the stack.
We move from state q0 to q1.
On the state q1, we are not supposed to see input symbols a., so we did not mention a transition about ‘a’ on q1.
On the state q1, If we see the input symbol b and the stack top is a, we pop the stack top element.
On the state q1, if the input symbol is epsilon and the stack top is z, we do no operation.
Push down automata can be represented using seven tuples (Q, Σ, τ, δ, q0, Z, F)
Q Finite set of states.
Σ Finite set of input symbols.
τ Finite set of stack symbols
q0 is the initial state
Z is the stack start symbol
F finite set of final states.
δ Transition Function
δ : Q X (Σ ∪ {ε}) X τ -> Q X τ*
A move in PDA may indicate.
a) one element may be added to the stack
b) one element may delete from the stack.
c) may not be changed in the stack
In all these moves, the state may or may not change.
