Axioms of Probability
In this class, We discuss Axioms of Probability.
For Complete YouTube Video: Click Here
The reader should have prior knowledge of probability basics. Click Here.
Axiom 1: For any event, A
P(A) >= 0
The event which is unlikely to happen P(E) ≈ 0
Example: E = Randomly select card ‘5’ of spade
P(E) = 1/52
The event likely to happen P(E) ≈ 1
Example: E = Randomly pick spade or red card.
P(E) = 39/52
Axiom 2:
Probability of sample space S = 1
Definitely one of the possibility from the sample space will happen.
Example: Toss two coins
S = {HH, HT, TH, TT}
P(S) = 1
100% one from the sample space will happen
Axiom 3:
If A1, A2, A3, . . . An are disjoint events.
P(A1 U A2 U . . An) = P(A1) + P(A2) + . . P(An)
Example: Toss two coins
S = {HH, HT, TH, TT}
E1 = {HH}
E2 = {HT}
E1 and E2 are disjoint events.
P(E1 U E2) = P(E1) + P(E2)
P(E1 U E2) = 1/4 + 1/4 = 1/2
Without using the Axiom
E = {HH, HT}
P(E) = 2/4 = 1/2
Not Disjoint Events
Addition law of probability
P(E1 U E2) = P(E1) + P(E2) – P(E1 ∩ E2)
Example: Roll a dice
E1 = dice show even number = {2, 4, 6}
E2 = dice show value greater than three = {4, 5, 6}
The below Venn diagram of events E1 and E2 are not disjoint sets.
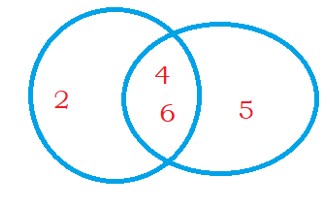
P(E1) = 3/6
P(E2) = 3/6
P(E1 ∩ E2) = 2/6
The numbers 4 and 6 are involved in the probability of events E1 and E2.
One time is enough. So we are subtracting P(E1 ∩ E2)
Similarly, P(E1 U E2 U E3) = P(E1) + P(E2) + P(E3) – P(E1 ∩ E2) – P(E1 ∩ E3) – P(E2 ∩ E3) + P(E1 ∩ E2 ∩ E3)
Example: Roll a dice
A = {1, 2, 5}
B = {2, 5, 6}
C = {5, 6, 3}
the common element is 5
P(A) = 3/6 the element 5 involved
P(B) = 3/6 the element 5 involved
P(C) = 3/6 the element 5 involved
P(A ∩ B) = 2/6 the element 5 involved
P(A ∩ C) = 1/6 the element 5 involved
P(B ∩ C) = 2/6 the element 5 involved
P(A ∩ B ∩ C) = 1/6
P(A U B U C) = P(A) + P(B) + P(C) – P(A ∩ B) – P(A ∩ C) – P(B ∩ C) + P(A ∩ B ∩ C)
We added the term P(A ∩ B ∩ C) to involve element five.
Complement Law:
P(E’) = 1 – P(E)
P(E) + P(E’) = 1
P(E) + P(E’) = P(S)
