Bernoulli Distribution with Example

In this class, We discuss Bernoulli Distribution with Example.

For Complete YouTube Video: Click Here

The reader should have prior knowledge of probability distributions. Click Here.

Bernoulli Distribution:

Bernoulli distribution is a discrete probability distribution with only two possible outcomes.

One outcome we call success or 1

Another outcome is Failure or 0

Example:

Toss a coin.

The outcomes are head or tail.

Head is considered a success.

Tail is considered a Failure.

Important: Roll a dice is considered as bernoulli distibution.

Outcome 6 is considered a success.

The other outcomes are considered Failure.

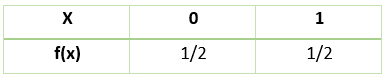
Bernoulli probability distribution table:

Toss a coin.

Success = head

The below table shows the probability distribution.

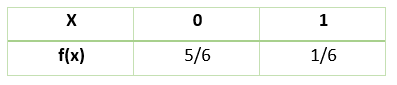
Roll a dice.

success = 6

Failure = 1, 2, 3, 4, 5.

The below table shows the probability distribution.

Bernoulli probability distribution graph

The below diagram shows the probability distribution graph for rolling dice.

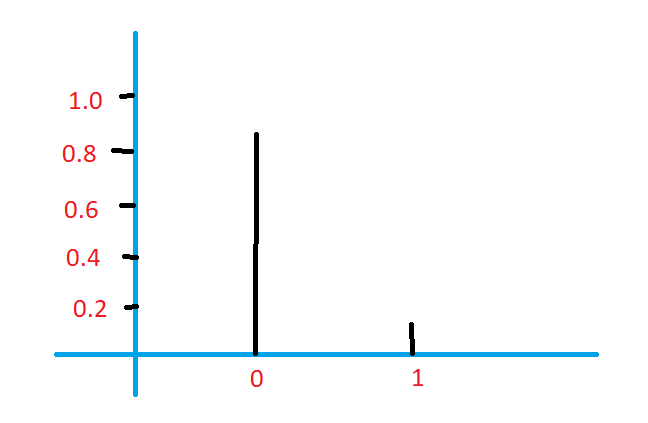
On the X-axis, we take 0 and 1.

On the Y-axis, we take the probability values.

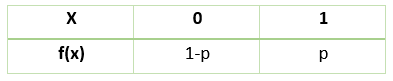
If P(success) = p for a bernoulli distribution then P(Failure) = 1-p.

Probability Mass Function for Bernoulli Distribution:

PMF = P^x(1-P)^1-x

PMF = f(x)

Why the above PMF?

f(0) = 1-P

f(1) = P

Expected value of Bernoulli distribution.

E(X) = all x Σ xf(x)

= 0(1-P) + 1(P)

= P

Variance of Bernoulli Distribution:

Variance = E(X2) – (E(X))2

= P – P2

= P(1-P)