Mutually Exclusive and Complement Events

In this class, We discuss Mutually Exclusive and Complement Events.

For Complete YouTube Video: Click Here

The reader should have a prior understanding of basic probability examples. Click Here.

Mutually Exclusive Events:

Two events, E1 and E2. Occurring of both events at the same time is not possible then the two events are mutually exclusive.

Example: Roll a dice

Event E1: Dice should show an even number.

E1 = {2, 4, 6}

Event E2: Dice should show an odd number.

E2 = {1, 3, 5}

When we roll a dice, the dice may show even or odd. But not both.

The events E1 and E2 are mutually exclusive.

The below diagram shows the Venn diagram for events E1 and E2.

The two events E1 and E2 are disjoint sets.

Not Mutually Exclusive Events:

Event E1 = Dice should show Even numbers

Event E2 = Dice should show a value greater than three

E1 = {2, 4, 6}

E2 = {4, 5, 6}

The below Venn diagram shows the sets E1 and E2.

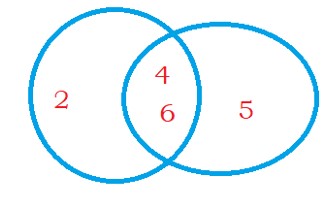
The intersection of two sets is E1 ∩ E2 = {4, 6}

The two events can happen at the same time.

Complement Events:

Toss two coins.

The sample space S = {HH, HT, TH, TT}

Even E = {HH}

Complement of event E = E’ = {HT, TH, TT}

E’ = Remaining elements in the sample space.

Important: E U E’ = S