Probability Distribution Expected Value Examples
In this class, We discuss Probability Distribution Expected Value Examples.
For Complete YouTube Video: Click Here
The reader should have prior knowledge of the expected value. Click Here.
Example 1:
Toss dice three times.
We consider success as tossing 1 or 6.
Find the mean of the success?
Solution:
Random variable X = Number of success.
X = { 0, 1, 2, 3}
P(success) = P(S) = 2/6 (Tossing 1 or 6 is a success)
P(Failure) = P(F) = 1 – 2/6 = 2/3
P(X = 0) = P(zero success) = 2/3 * 2/3 * 2/3
P(X = 1) = (1/3 * 2/3 * 2/3) + (2/3 * 1/3 * 2/3) + (2/3 * 2/3 * 1/3)
P(X = 2) = (1/3 * 1/3 * 2/3) + (1/3 * 2/3 * 1/3) + (2/3 * 1/3 * 1/3)
P(X = 3) = (1/3 * 1/3 * 1/3)
The below table shows the probability distribution of random variable X.
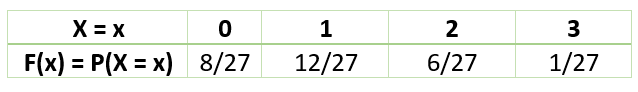
E(X) = Σ 0 to 3 (xi pi)
E(X) = (0 * 8/27) + (1 * 12/27) + (2 * 6/27) + (3 * 1/27)
E(X) = 1
Example 2:
Two dice are thrown.
Random variable X = Max(First dice value, Second dice value).
Find the probability distribution and mean.
Solution:
X = {1, 2, 3, 4, 5, 6}
P(X = 1) = {1, 1} = 1/36
We take maximum value 1 in the event {1, 1}.
P(X = 2) = {(1,2), (2,2), (2,1)} = 3/36
P(X = 3) = 5/36
P(X = 4) = 7/36
P(X = 5) = 9/36
P(X = 6) = 11/36
The below table shows the probability distribution.

E(X) = (1 * 1/36) + (2 * 3/36) + (3 * 5/36) + (4 * 7/36) + (5 * 9/36) + (6 * 11/36)
E(X) = 4.47
