Properties of Normal Distribution

In this class, We discuss the Properties of Normal Distribution.

The reader should have prior knowledge of normal distribution. Click Here.

We take an example and understand the properties of normal distribution.

Example:

Take students’ probability and statistics subject marks distribution.

The marks distribution follows the normal distribution.

Mean = µ = 55

Standard deviation = σ = 10

The below diagram shows the probability distribution of marks.

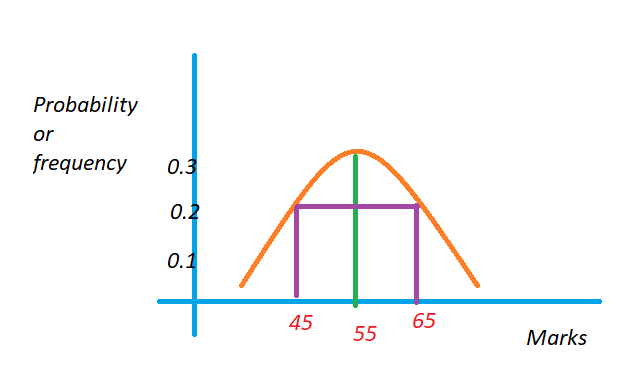
On the x-axis, we take marks, and on the y-axis, we take probability values.

Property 1:

Always normal distribution is symmetric. Why?

Take the normal distribution probability density function.

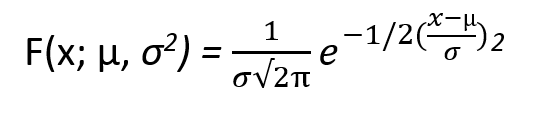
Take two random variables x = 45 and 65.

The two random variables are ten units from the mean value of 55.

substitute the values in the probability density function. We will get the same value.

x = 45 we get ((45 -55)/10)^2 = 1

we are considering the part ((x- µ)/σ)^2 from the PDF. The remaining part is the same for any random variable.

x = 55 we get ((55-65)/10)^2 = 1

Property 2:

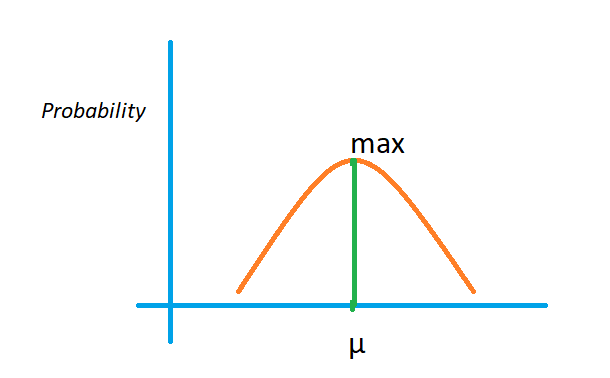
Maximum probability occurs at the mean value.

If the random variable x = µ substitute in the PDF, we get 1/σ√2π.

The maximum value obtained at the random variable x = µ.

The below diagram shows the maximum value at the mean.

Property 3:

Mean = Median = Mode for normal distribution.

Mode means to pick the highest frequency value. The highest frequency is at the mean.

The normal distribution is symmetric, so the median is at a center point, the mean value.

Important:

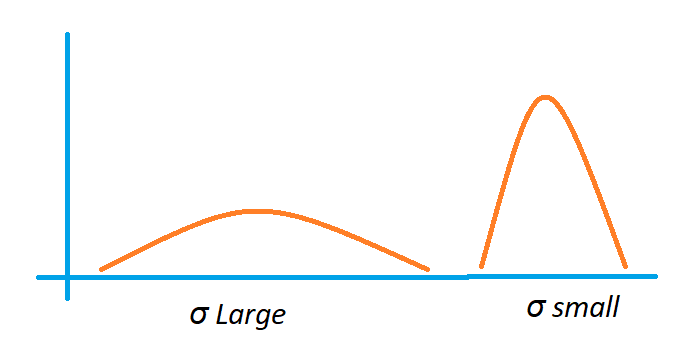
We obtain the maximum value at the mean. The value is 1/σ√2π.

As σ is small, the 1/σ√2π value is large.

As σ is large, the 1/σ√2π is small.

σ means standard deviation.

The below diagram shows the change in the shape of the normal distribution with standard deviation.

Property 4:

The normal distribution has different sizes and shapes based on the µ and σ values. But there is one and only one normal distribution for any µ and σ value.

With an example, we will understand property 4.

The below diagram shows the two normal distributions.

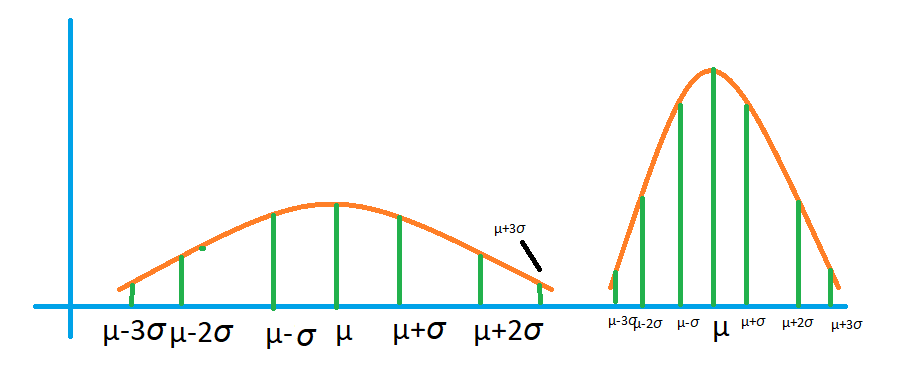
Take two normal distributions.

The first distribution with µ = 15 and σ = 5.

The second distribution with µ = 25 and σ = 2.5.

Take the values µ–σ. I.e., one standard deviation away from the mean value to the left.

µ+σ is one standard deviation from the mean value to the right.

Similarly, µ+2σ is two standard deviations away from the mean.

Take any normal distribution.

The area between µ–σ to µ+σ is 68 percent.

The area between µ-2σ to µ+2σ is 95 percent.

The area between µ–3σ to µ+3σ is 99.7 percent.

Property 5:

Always the probability value for the normal distribution is greater than zero.