Quartiles and its Uses

In this class, We discuss Quartiles and its Uses.

For Complete YouTube Video: Click Here

The reader should have prior knowledge of the measure of central tendency. Click Here.

Quartiles:

Quartiles are three points that divide the data series into four equal parts.

Example:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12

Total, we have n observations.

n = 12 in our example

Q1, Q2, and Q3 are quartile points.

The three points, Q1, Q2, and Q3, divide the data into four equal parts.

Q1 is our first quartile point.

25% of the data is left of the quartile value.

Q2 is our second quartile.

50% of the data is left in the quartile Q2.

Q2 is called the median quartile.

Q1 is called the lower quartile.

Q3 is called the upper quartile.

Q1 = ((n +1)/4)th observation

Q2 = ((n +1)/2)th observation

Q3 = (3(n +1)/4)th observation

Use of quartile points

Simply finding the measure of central tendency will not help much in data analysis.

The quartile points help in a deeper understanding of data.

Example: Marks in a class

45, 46, 47, 48, 52, 55, 59, 62, 68, 69

The quartiles help to identify poor students and good students

Quartile points in a symmetric distribution

The below diagram shows the symmetric distribution

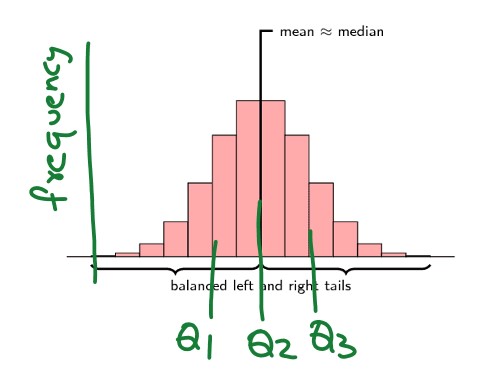
This graphical intuition helps readers to understand the next classes.

Quartiles in asymmetric distribution.

The below diagram shows the asymmetric distribution.

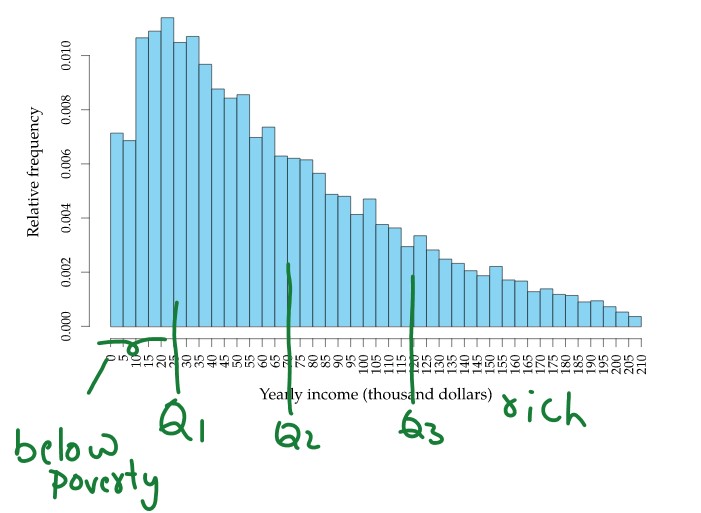
The data before the lower quartile are below the poverty line.

The data after the upper quartile are rich.