Quartiles Given Frequency Distributions
In this class, We discuss Quartiles Given Frequency Distributions.
For Complete YouTube Video: Click Here
The reader should have prior knowledge of quartiles and their uses. Click Here.
For continuous interval frequency distribution
Q1 = L + (h/f)((N/4)-c) lower quartile
Q2 = L + (h/f)((N/2)-c) median quartile
Q3 = L + (h/f)(3(N/4)-c) upper quartile
The above-median quartile equation is explained when we discussed the median for frequency distribution.
Example:
Eight coins are tossed together at random.
The number of heads is recorded.
The experiment was repeated 256 times, and the frequency for showing the head is in the table.
Find the quartile points.
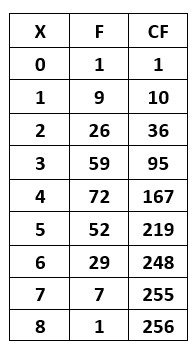
N = 256
Q1 = N/4 = 64
Q2 = N/2 = 128
Q3 = 3N/4 = 192
The lower quartile value is three because 64 comes to X value 3.
The median quartile value is four because 128 comes to an X value of 4.
The upper quartile value is five because 192 comes to an X value of 5.
Example 2: Continuous class
The below table shows the data distribution.
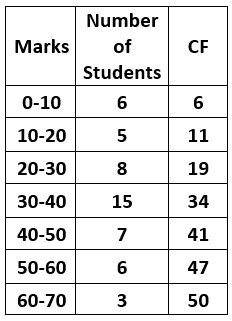
N/4 = 50/4 = 12.5 = 13
Q1 = class 20 – 30
N/2 = 50/2 = 25
Q2 = class 30 – 40
3N/4 = 150/4 = 37.5 = 38
Q3 = class 40 – 50.
The quartile value should be a value between the lower and upper values of the class.
Q1 = L + (h/f)((N/4)-c) lower quartile
Q1 = 20 + (10/8)(12.5 – 11)
Q1 = 21.8
The reader can do the remaining quartile points.
